Blog

Will This Be on the Test? (September 2024)

by Sarah Lonberg-Lew

---

Welcome to the latest installment of our monthly series, “Will This Be on the Test?” Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually.

---

Welcome back to our continuing exploration of how to bring real conceptual reasoning to questions students might encounter on a standardized test.

I recently saw a video on YouTube that purported to “teach” students how to find the equation of a line in slope-intercept form given two points by using a TI-30XS (the calculator provided for the GED). Maybe you’ve seen the same video or a similar one. There is no shortage of videos online teaching how to do specific types of math problems on the calculator. The sequence of buttons to press was long and convoluted and I got a headache just imagining trying to memorize it. And that was all for one single specific question-type. It got me thinking about what other approaches might be less painful, more grounded in sense-making, and more generalizable to other tasks.

So here’s this month’s question. Can you figure it out without reaching for a calculator or relying on a memorized procedure?

You may recognize that for a question like this, it is very helpful for a student to know the meanings of slope and y-intercept and how they show up an equation that’s written in slope-intercept form. For the purpose of this exploration, let’s assume that understanding. Here are some visual and conceptual approaches that a student could take.

1. Start with a rough sketch. Drawing a quick sketch of the line through the two given points will reveal quite a lot of useful information. Students may or may not find it helpful to draw tick-marks on their sketch.

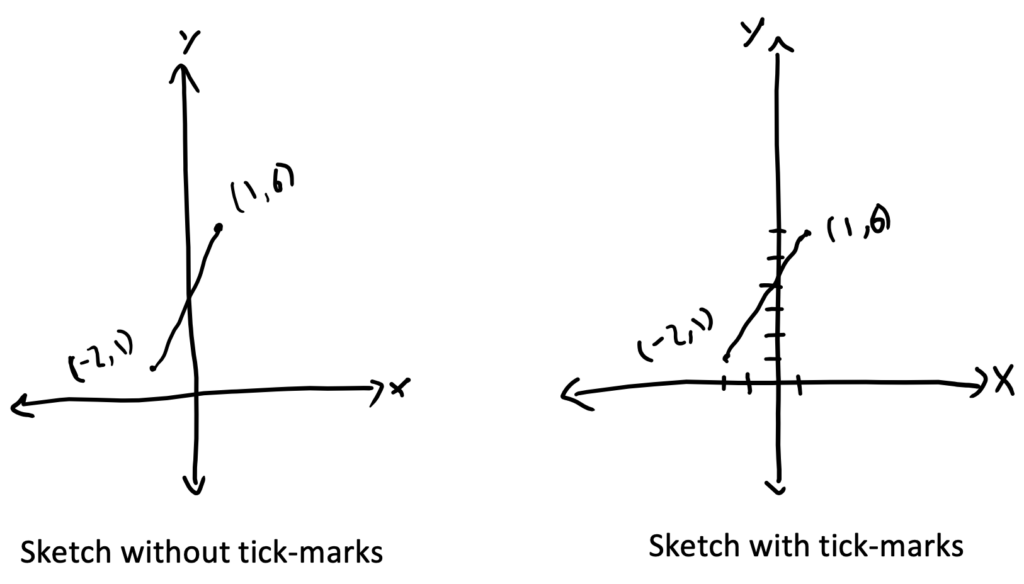
What do you notice about the sketches? What information can you glean about the slope? What information can you glean about the y-intercept? Which answer choices seem reasonable or unreasonable now? (If students get in the habit of drawing sketches, they will grow their ability to make sketches that are roughly to scale and can give them useful information for estimating or eliminating answer choices. This also will build conceptual understanding of the meaning of slope and y-intercept.)

2. Reason visually about the slope. From the rough sketch, we can see that the slope is positive. A student might eyeball whether it appears to be a steep slope or a shallow one, but they might also want more precise information. Instead of using a formula, a student who understands that slope is a ratio used to measure the steepness of a line might reason more like this:

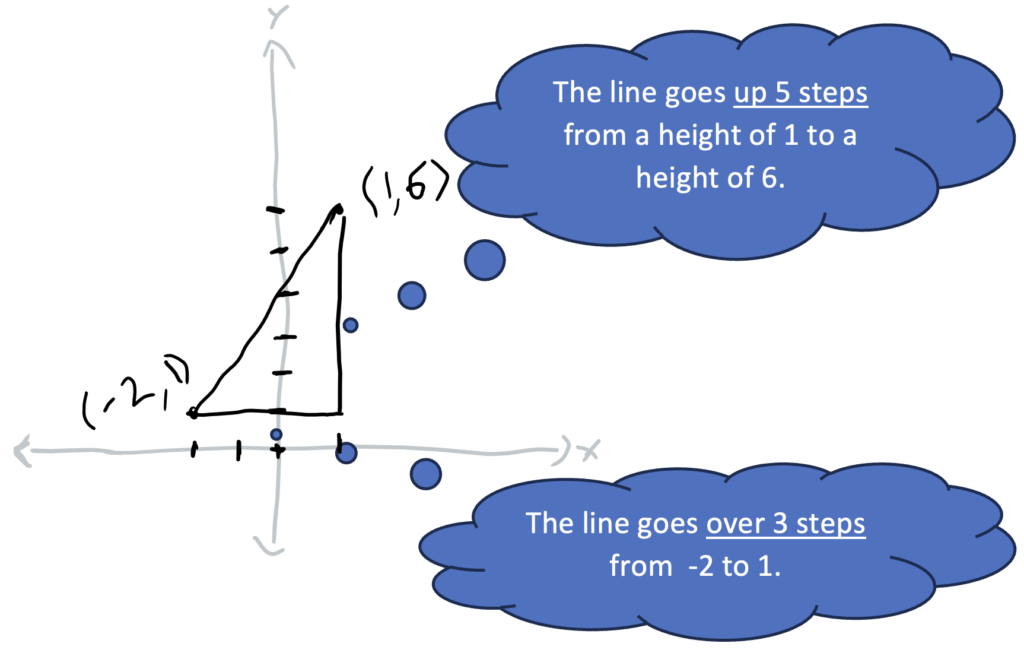
Knowing that the slope is positive, finding the slope becomes a matter of thinking about distances on a number line or counting tick-marks. It isn’t necessary to remember rules for subtracting signed numbers or make sure you subtract in the same direction for both coordinates. A student only needs to find the distances (in whatever way makes sense to them) and assign a positive sign to the ratio. In this case, the slope is positive 5/3 because the line goes up 5 and over 3 and it is a positive slope. (For more ideas about thinking about slope, see the May 2024 installment of Will This Be on the Test.)

3. Use slope steps from one of the points to find the y-intercept. We can interpret the slope of 5/3 in different ways. One way is to understand that if we start at one point on the line and move over 3 and up 5, we will arrive at another point on the line. Another is to understand that every step of size 1 in the x direction corresponds to a step of size 5/3 in the y direction. (If you’re not sure whether to move left or right or up or down, a picture will help.) Using this second understanding, a student could start at one of the points we were given and use slope steps to get to the y-axis. For example, one of the given points is (-2,1). Looking at one of the sketches, we can see that it is a distance of 2 horizontal steps from the y-axis. Therefore, to get to the y-intercept, we will move over 2 steps horizontally and up 5/3 steps for each horizontal step. So, we will move up 5/3 steps twice, putting the y-intercept at 1 + 5/3 + 5/3.

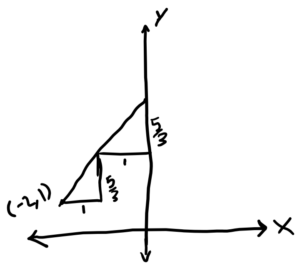
Could a student choose, instead, to find the y-intercept by taking slope steps from the other given point? How would that be similar to or different from this approach?

By the time students get to topics like slope-intercept form of a line, it may be tempting to start with an algebraic procedure (or several) and rely on memorizing the steps of that procedure. However, regardless of a student’s level—or regardless of your own level when you are trying to learn a new concept—it makes a big difference to start with what is concrete and/or visual and build to abstract thinking. Starting with an abstract algebraic procedure can be as meaningless to students as trying to memorize a sequence of calculator buttons. If students start with conceptual understanding at the concrete or visual level, they will move to abstract and symbolic thinking naturally when they are ready, and they won’t be bound to a specific procedure but will instead be able to use their flexibility and algebraic reasoning to answer many types of questions.

---