Will This Be on the Test? (November 2024)

by Sarah Lonberg-Lew

Welcome to the latest installment of our monthly series, “Will This Be on the Test?” Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually.

Welcome back to our continuing exploration of how to bring real conceptual reasoning to questions students might encounter on a standardized test.

One question that comes up often when I am talking with teachers is deciding how much time to devote to learning how to do fractions on the calculator and how much time to devote to learning fraction reasoning. Because calculators are allowed on some or all of the questions on high school equivalency tests, and because developing real conceptual understanding about fractions takes time, it often seems more expedient to focus on the calculator. When I take the long view, though, I can’t help but think that time spent learning to do fraction operations on one specific calculator is not of the greatest value to students. The calculator steps are unintuitive and cumbersome and not easy to learn, and when there is no conceptual understanding behind the button-pushing, students are not equipped to know whether they have gotten a reasonable answer.

I recently came across a question in a published practice test that showed me that sometimes the test-makers are trying to find ways to assess fraction reasoning even when students have a calculator. This month’s question is adapted from that question. As you think about it, consider how a calculator might or might not be useful.

Here’s this month’s question:

Which fraction is closest to the sum of ⅜ + 1/5? Answer options: ⅜, 4/9, 3/5, ⅝, or ⅔

How can you approach this question in a way that makes sense to you? What conceptual understandings or visual tools can you bring to bear? What mathematical concepts do students really need to be able to tackle this problem? How might your real-world experience help you reason about this?

Here are some possible approaches:

1. Estimate with benchmarks. Finding the sum of the given fractions is only part of the task for this question. The other part is to figure out which of the answer choices is closest to that sum. In other words, a student who knows how to find the sum procedurally or on a calculator may not be able to finish the task if they are not able to reason about the relative sizes of fractions.

In fact, a student who can reason about the sizes of fractions can find an entry point into this question even if they don’t know how to add fractions by reasoning about benchmark fractions. A student might look at the given sum and ask, “Is it closer to 0, 1/2, or 1?”

A bar model fraction diagram can make this easier to think about:

Start with a picture of 3/8, which is pretty close to 1/2 because it would only take one more block to make 1/2.

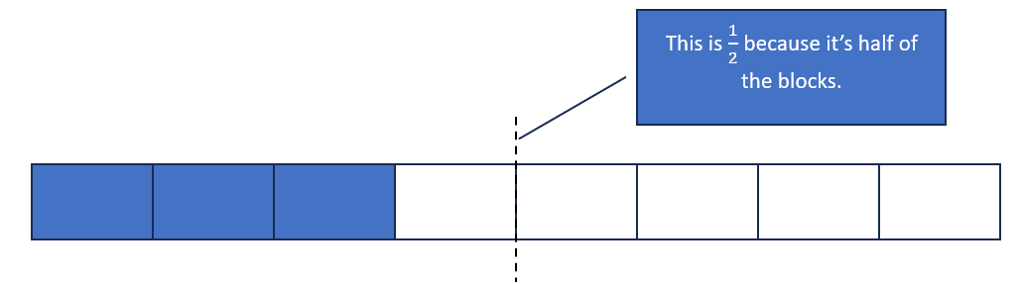
A fraction bar diagram showing three blue rectangles and five white rectangles. A label points to a line marking the fourth rectangle and reads, "This is one half because it's half of the blocks."

Would adding 1/5 push it over the halfway mark?

Since adding 1/8 would make it exactly half, we can ask whether 1/5 is bigger or smaller than 1/8.

Two pie charts, one divided into 5ths and one divided into 8ths. A question bubble asks, "Which circle has bigger pieces?"

A student who understands the meaning of fractions will recognize that 1/5 is bigger than 1/8 because when you divide something into 5 equal pieces, you get bigger pieces than when you divide the same thing into 8 equal pieces.

(This is an understanding that students may take time to solidify for themselves because it feels a little counterintuitive—bigger denominators make smaller fractions—but it is important that students have that time to make sense of this because it underlies all kinds of fraction reasoning.)

So now we know that adding 1/5 adds more than the size of one block on the diagram. But does it add more than two blocks? Two blocks is 2/8 or 1/4, and 1/5 is not as big as 1/4 because fourths are bigger than fifths. (There’s that fundamental fraction understanding again.)

So adding 1/5 adds more than the size of one block, but less than the size of two blocks. Visually, we can say that the sum of 3/8 + 1/5 is somewhere in that fifth block to the right:

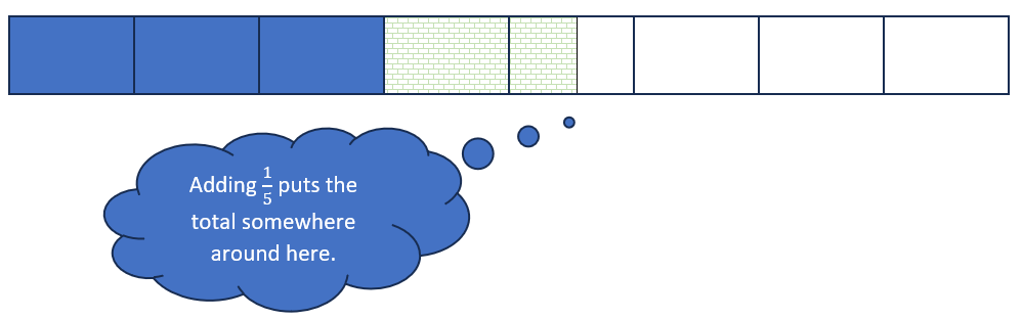
A fraction bar diagram showing three eighths with three blue blocks and five white blocks. There is a green block superimposed that extends across between one and two of the white blocks at the end of the blue blocks. A label pointing to the end of the green block reads "Adding one fifth puts the total somewhere around here."

Looking at the answer choices, which seem like they might be around that same place? It may help to sketch some of them or think about how close they are to 0, 1/2, or 1.

2. Consider differences/distances from answer choices without adding. Another possible approach is to consider some of the answer choices that have friendlier denominators (in this case 5 or 8 because they already match one of the numbers in the sum) and think relationally about how they compare to the sum. For example, answer choice (A) is definitely less than the sum because 3/8 must be less than 3/8 plus another piece. (How far away is it from 3/8 +1/5? Can you tell without adding?)

Another one that is accessible to compare is 3/5, which is bigger than 1/5 by 2/5. In other words, you can get 3/5 by adding 2/5 to 1/5 to How does adding 3/8 compare to adding 2/5? It can help to compare them each to 1/2: 

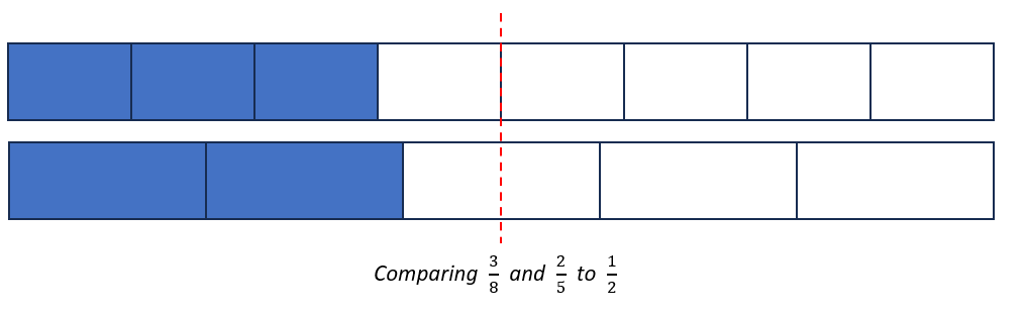
A bar model diagram showing three eighths above a bar model diagram showing two fifths. A dotted line shows the location of one half on both models. There is text underneath that reads, "comparing three eighths and two fifths to one half."



3/8 and 2/5 are both a little less than half, so even though they are not equal, they are close in size.

3. Do the addition and compare to the answer choices. As you can see from the previous strategy, it may not be necessary to find the sum at all in order to feel confident about your answer choice. However, a student may also find the sum and then try to compare it to the answer choices. This is a place where a calculator may make things a little quicker in finding the sum, but the calculator likely will not be that much use in deciding which of the answer choices is closest to the sum. The sum of the fractions (however you find it) is 23/40. Looking at the answer choices, which seem easier to compare to that sum? Answer choices (A), (C), and (D) all have denominators that can be converted to 40ths without too much work. Those might be good choices to start with.

So, is it worth spending classroom time building skill with fraction operations on a calculator? My opinion is that that time is better spent on reasoning. First of all, the test makers can and do create questions for which knowing how to do the operations on a calculator is not enough. Also that we have so little time with our students and when we use that time to build conceptual understanding we help students grow their brains, grow as independent learners, and learn math skills that they may even transfer to their lives outside the classroom. (Think about the fraction reasoning involved in thinking about nutrition information, time, measurement, representations of data… fractions do exist in our lives!) When we spend our precious time on learning calculator button sequences, all students learn is calculator button sequences – something that will only be useful to them on the test, and may not even stick with them in that situation if they have learned it with no meaning attached.

Sarah Lonberg-Lew has been teaching and tutoring math in one form or another since college. She has worked with students ranging in age from 7 to 70, but currently focuses on adult basic education and high school equivalency. Sarah’s work with the SABES Mathematics and Adult Numeracy Curriculum & Instruction PD Team at TERC includes developing and facilitating trainings and assisting programs with curriculum development. She is the treasurer for the Adult Numeracy Network.