Will This Be on the Test? (January 2025)
by Aren Lew
Welcome to the latest installment of our monthly series, “Will This Be on the Test?” Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually.
Welcome back to our continuing exploration of how to bring real conceptual reasoning to questions students might encounter on a standardized test.
Here’s a classic to start the new year. It may be a classic question, but that doesn’t mean we can’t approach it creatively. Can you think of ways to approach it that don’t involve applying a memorized formula?
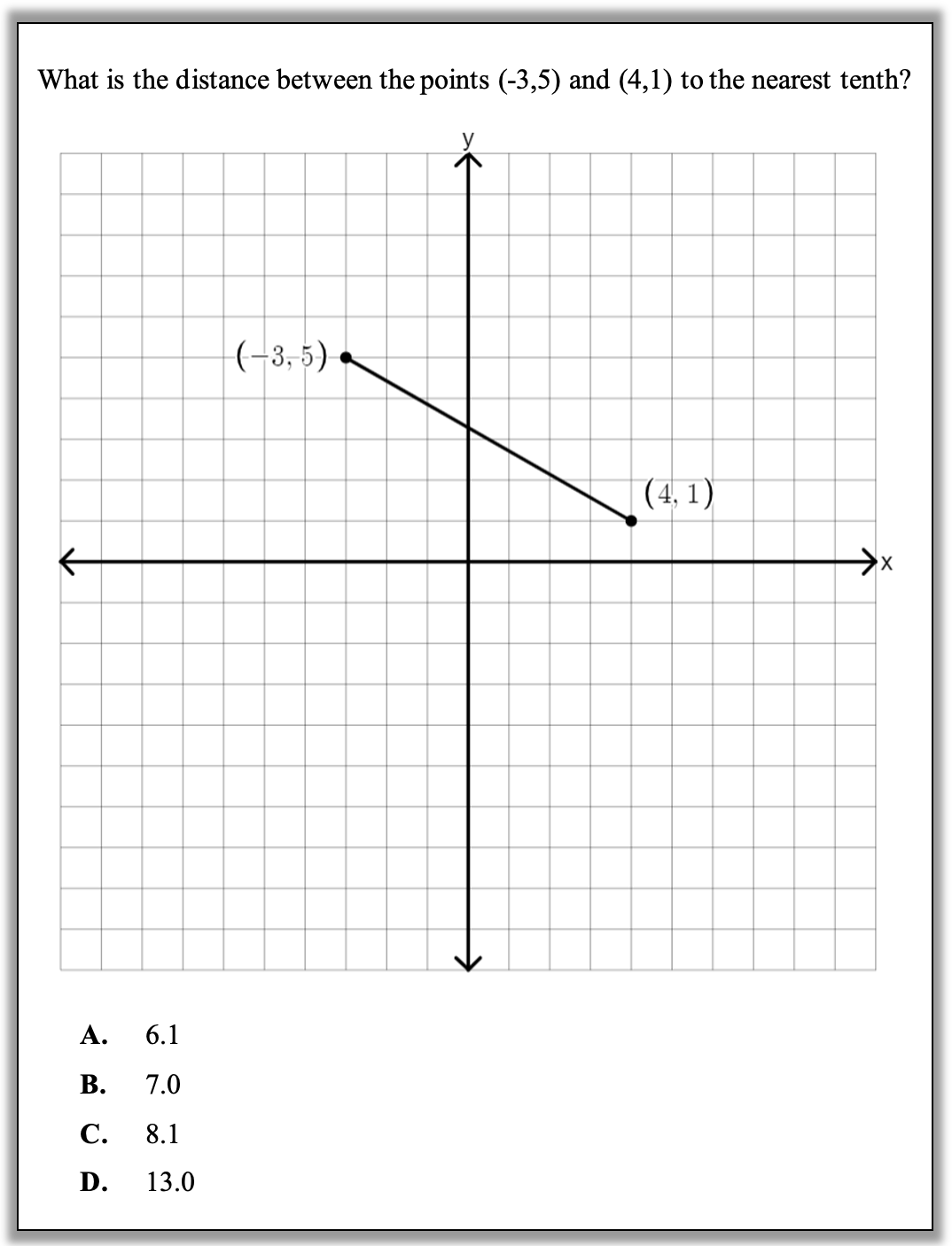

How can you approach this question in a way that makes sense to you? What conceptual understandings or visual tools can you bring to bear? What mathematical concepts do students really need to be able to tackle this problem? How might your real-world experience help you reason about this?
Here are some possible approaches:
1. Estimate! Eyeball the distance. A good starting place is just to see how long that line segment looks. Take a minute to try it yourself. Given that each grid square is one unit wide and one unit tall, how many units does the line appear to be?
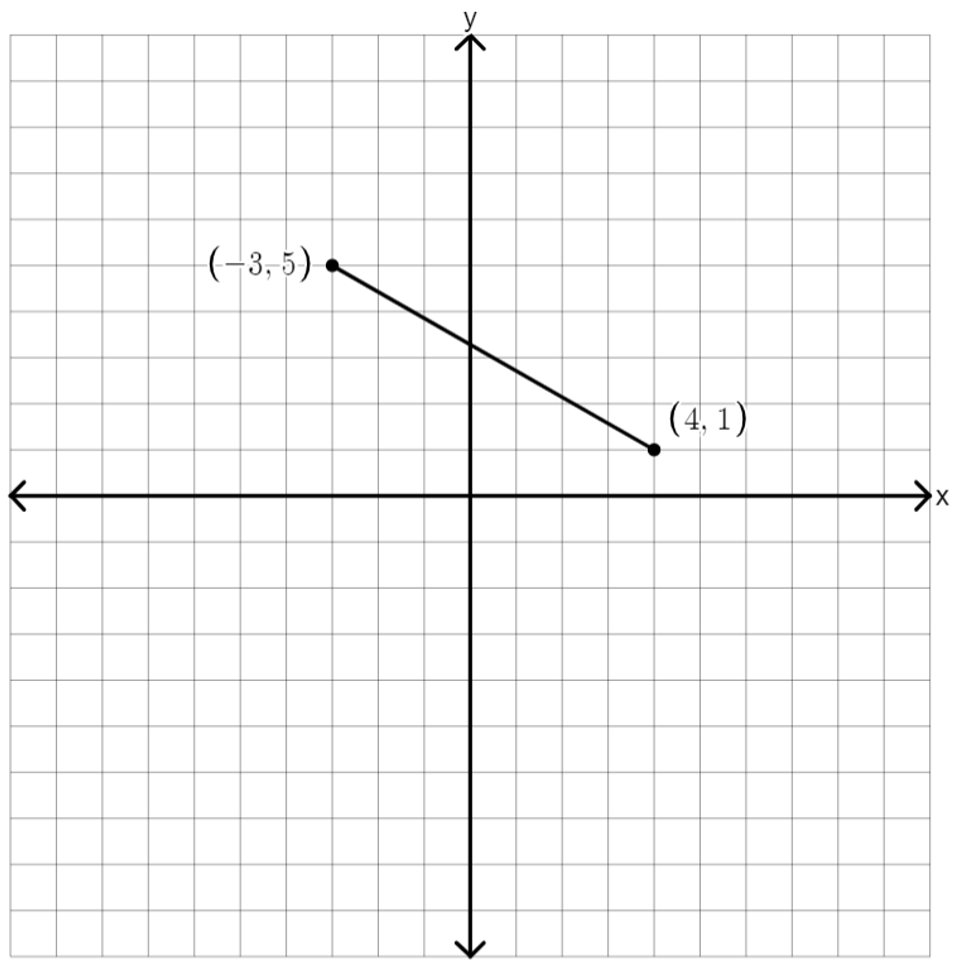
Here are a few ideas that might help with your estimate:
- Can you picture rotating the line up or down so that it is horizontal or vertical? You might rotate it from the point on the left or the one on the right or maybe from somewhere in the middle.
- Can you imagine putting tick marks along the line that are spaced the same as the grid lines?
- Are there any answer choices that seem definitely too big or definitely too small?
2. Build a triangle and estimate based on triangle relationships. One of the most powerful tools in a mathematician’s (that’s you and your students!) toolbox is marking up diagrams to give you more tools for thinking. In this case all that we’re given in a line segment, but we can build a triangle on the grid lines that will give us more information, like this:
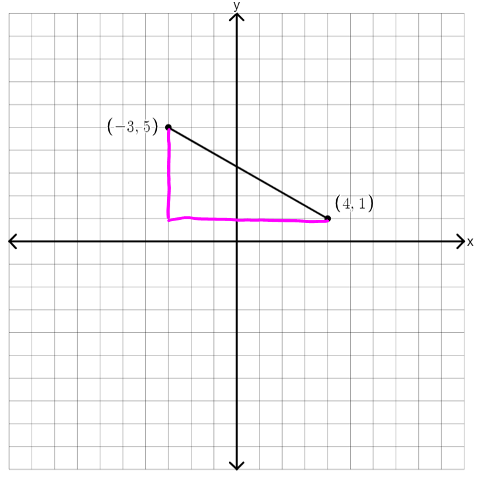
Now you can think specifically about how the length we are seeking compares to the other lengths in the triangle (which we can measure by counting the boxes).
- Does the distance we’re looking for seem to be the longest, shortest, or middle side of the triangle?
- How does it compare to the sum of the other two sides?
(If you investigate these questions, you may also want to consider how your conclusions might be generalized to other triangles. You may find some ideas that are useful in other contexts.)
3. Build a right triangle and use the Pythagorean Theorem. Did you notice that the triangle we built in the last strategy was a right triangle? If you know the Pythagorean theorem, you can get to a solution by applying it to the triangle. One way to find the lengths of the legs is to count the boxes in the diagram. You can also do it by subtracting the x-coordinates and to the y-coordinates. It may not be obvious that subtraction can be a “distance between” operation. The distance between 5 and 1 is 4. The distance between ‑3 and 4 is 7. How might seeing these distances on the grid help students to make sense of subtraction with signed numbers?
Of course, there is a formula for solving a task like this. I learned it in school. It looks like this:
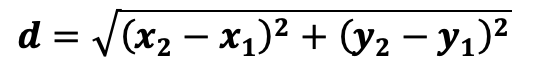
Subscripts and exponents and parentheses and square roots can make anyone want to run in the other direction from any question that requires you to apply this. As a student, I was able to use this to get correct answers reasonably consistently, but formulas are not reliable for everyone, and this one has lots of room for things to go wrong if you are using it without understanding. I have learned, though, to think conceptually about distances in the coordinate plane and I haven’t needed to pull out this formula since! Hopefully now you also have some tools for thinking about distance conceptually!
P.S. Some of the strategies here used the coordinate grid for thinking about distance. What if the grid lines had been missing or if there had been no diagram given at all? I challenge you to adapt the ideas in this post to those situations or to come up with your own strategies! (For use with students, a progression that starts with full grids, moves to diagrams with axes and no grids, and eventually just gives coordinates could help students see structure and patterns and move to more abstract thinking—just make sure not to rush it!)

Aren Lew has been teaching and tutoring math in one form or another since college. They have worked with students ranging in age from 7 to 70, but currently focus on adult basic education and high school equivalency. Aren’s work with the SABES Mathematics and Adult Numeracy Curriculum & Instruction PD Team at TERC includes developing and facilitating trainings and assisting programs with curriculum development. They are the treasurer for the Adult Numeracy Network.
