Blog

Will This Be on the Test? (February 2023)

by Sarah Lonberg-Lew

---

Welcome to the latest installment of our monthly series, “Will This Be on the Test?” Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually.

---

Welcome back to our continuing exploration of how to bring real conceptual reasoning to questions students might encounter on a standardized test. This month let’s dive into the surprisingly rich topic of the area and perimeter of rectangles. Here is this month’s problem:

One great thing about questions of area and perimeter is that students can find a way into them at different levels of abstraction. Some students may reason concretely about these concepts, using manipulatives like square inch tiles and string. Others may draw pictures, reasoning at a more representational level, and still others may reason abstractly, thinking about the quantities and relationships without drawing pictures or handling objects. Of course, students will not be able to bring square inch tiles or string into the testing environment, but working with them in the classroom will move them along the progression from concrete to representational to abstract. It will prepare them to work with drawings or abstract concepts when they get to the test.

Here are some possible approaches:

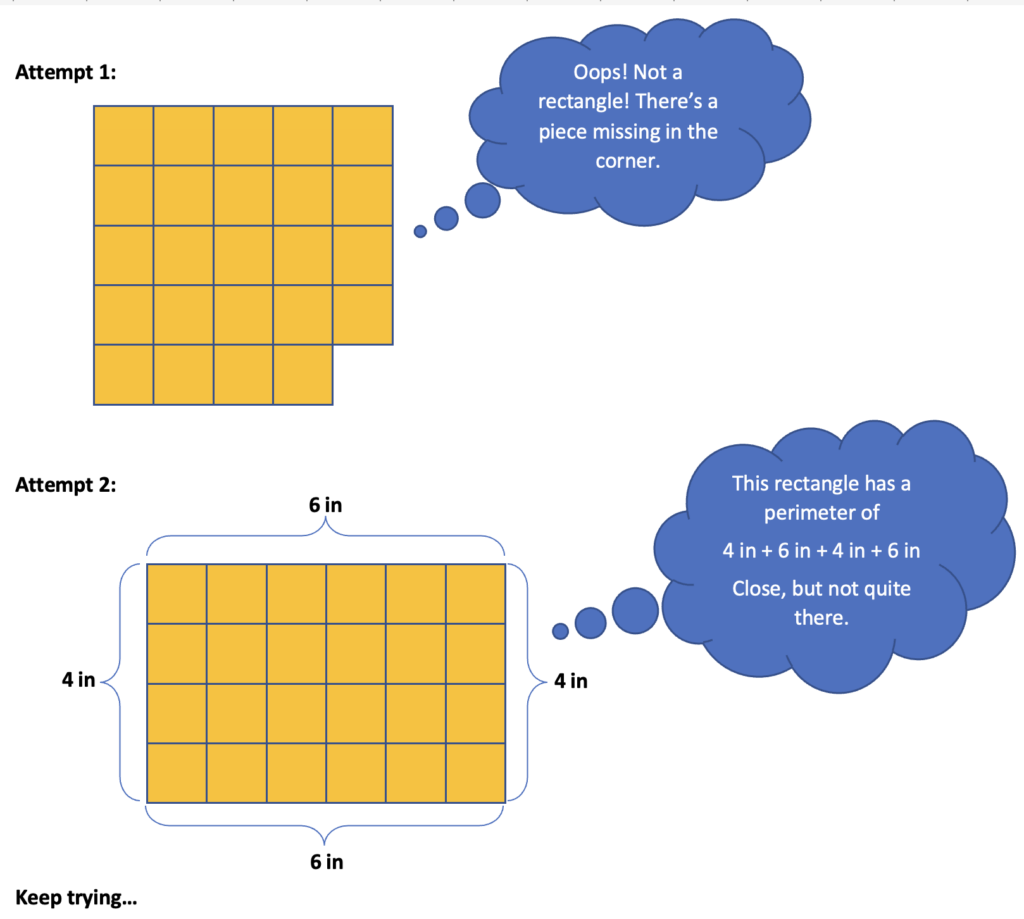
1. Play with area—concretely. Knowing that the area of the rectangle is 24 square inches, a student who is more comfortable reasoning at a concrete level might try using 24 squares to make a rectangle and then finding the perimeter like this:

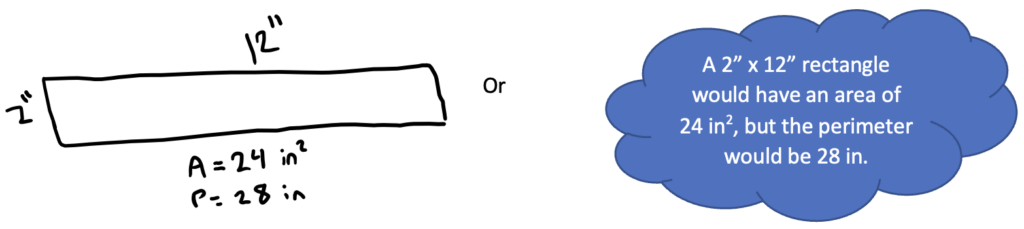
2. Play with area—representationally or abstractly. A student who is thinking more abstractly about area might make a rough sketch to get a handle on this question (or might reason without visuals at all):

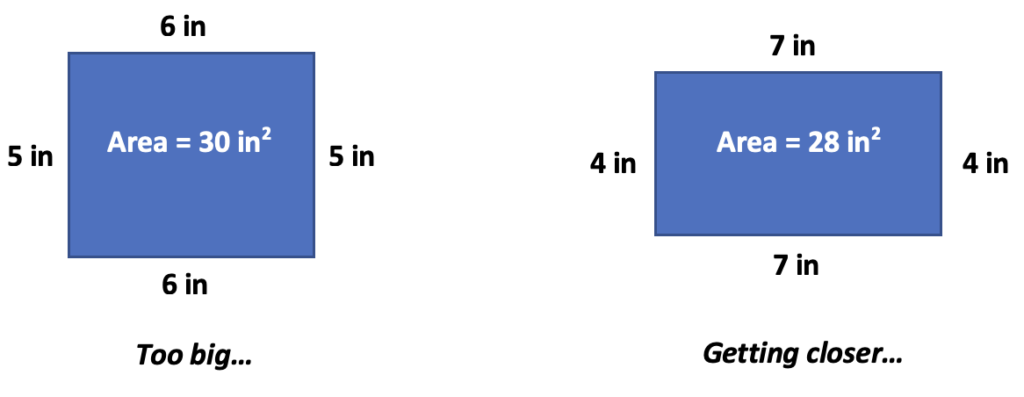
3. Play with perimeter. A student who is reasoning concretely and wants to start with the perimeter of the rectangle could cut a piece of string to 22 inches and then experiment with using it to create a rectangle on one-inch grid paper and counting the squares inside to check the area. A student reasoning more representationally might draw sketches of rectangles with perimeters of 22 inches and find their areas:

(It’s not that simple to create a rectangle with a given perimeter! Check out the free sample lesson: Understanding Perimeter with Formulas in the Curriculum for Adults Learning Math (CALM) for ideas on developing this concept.)

4. Make use of structure. Explorations with creating rectangles with a target perimeter may lead students to recognize a pattern in the relationship between the length and the width of a rectangle. Since the length and the width are each counted twice in the perimeter, just one of each must make half the perimeter. In other words, if the rectangle has a perimeter of 22 inches, the length and the width must add up to 11 inches. With this information, a student could make an organized table of possible dimensions to find the ones that yield the target area:

Length	Width	Area
1	10	10
2	9	18
…	…	…

This question involves higher level reasoning than a question that simply requires students to choose and apply a formula. It does involve higher level reasoning, but not higher level understandings. Any student who understands, conceptually, the meanings of area and perimeter can find an entry point into this task.

Area and perimeter can be a place where students struggle if their learning starts at the abstract level with formulas and procedures that are not connected to concrete objects or visuals. It can be easy to confuse the two ideas and not know which formula to use. In a question like the one we just looked at, students who only have learned how to plug values into formulas can be completely lost. However, when area and perimeter are taught conceptually and students are given the chance to construct their own formulas and strategies, they will be able to reason flexibly and take on all kinds of questions about them. 

---