Will This Be on the Test? (December 2024)
by Sarah Lonberg-Lew
Welcome to the latest installment of our monthly series, “Will This Be on the Test?” Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually.
Welcome back to our continuing exploration of how to bring real conceptual reasoning to questions students might encounter on a standardized test.
Teachers preparing students for an HSE test may choose to spend their geometry time on learning to identify and apply the formulas on the formula page. While making sense of the formulas can make them easier to recognize and use, it is also possible to reason out many geometry questions without going to the formula page. This month, let’s look at some alternatives.
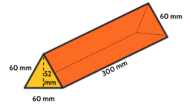
This month’s question comes from Three-Dimensional Geometry, Part 1, one of the many useful NYSED/CUNY Fast Track GRASP Math Packets:
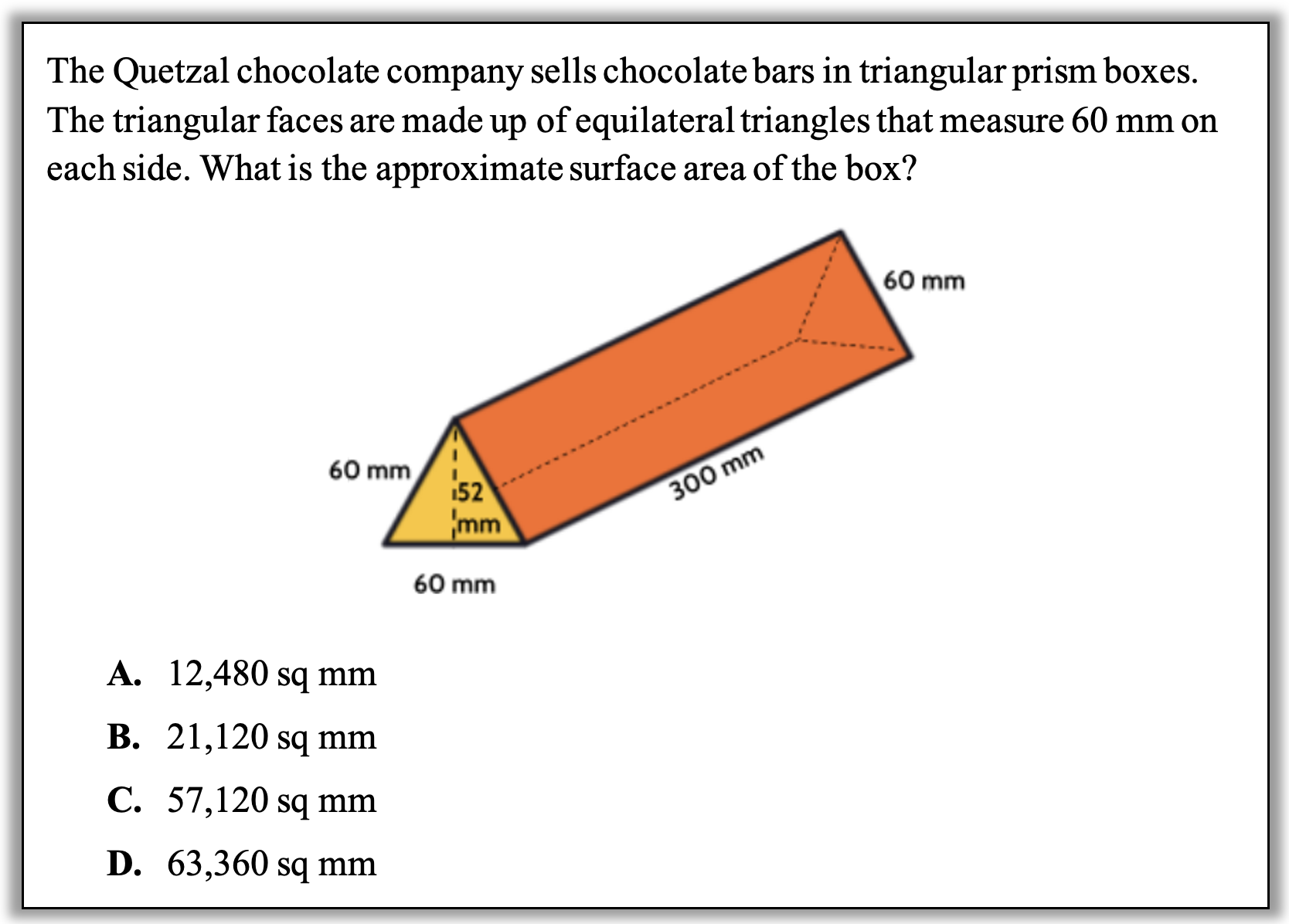

How can you approach this question in a way that makes sense to you? What conceptual understandings or visual tools can you bring to bear? What mathematical concepts do students really need to be able to tackle this problem? How might your real-world experience help you reason about this?
Here are some possible approaches:
1. Make sense of the question and estimate. There’s a lot of mathematical vocabulary in this question that might intimidate a student who is not familiar with it, but there is also a picture. While understanding the vocabulary of “triangular prism”, “triangular faces”, and “equilateral triangles” will definitely make this question more accessible, the only concept here that is absolutely essential is “surface area.” A student who understands the meaning of surface area as the total area of the outside of the box, or even more concretely as the amount of cardboard needed to make the box, has a way into making sense here. The first step can be restating the question:
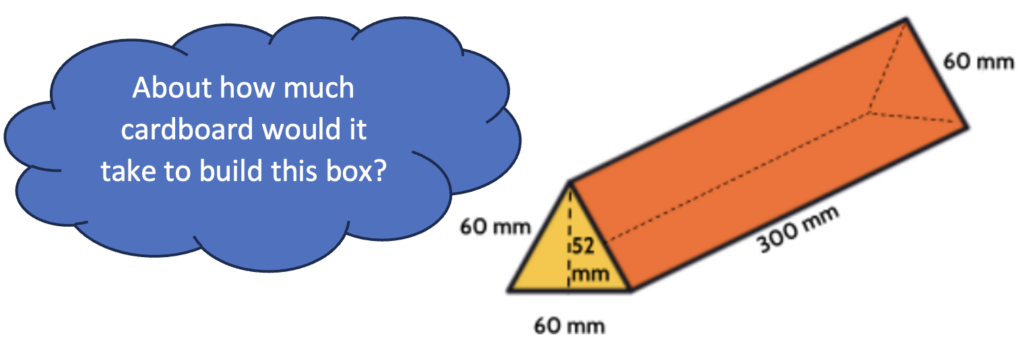
And a further step can be thinking about what pieces are needed to make the box. Being able to draw a net is useful, but not necessary here. Since the surface area is the total area of all the surfaces, all a student needs to be able to do is identify the surfaces. (This is a skill students can practice at home by taking apart cardboard containers like cereal boxes or other packaging.)
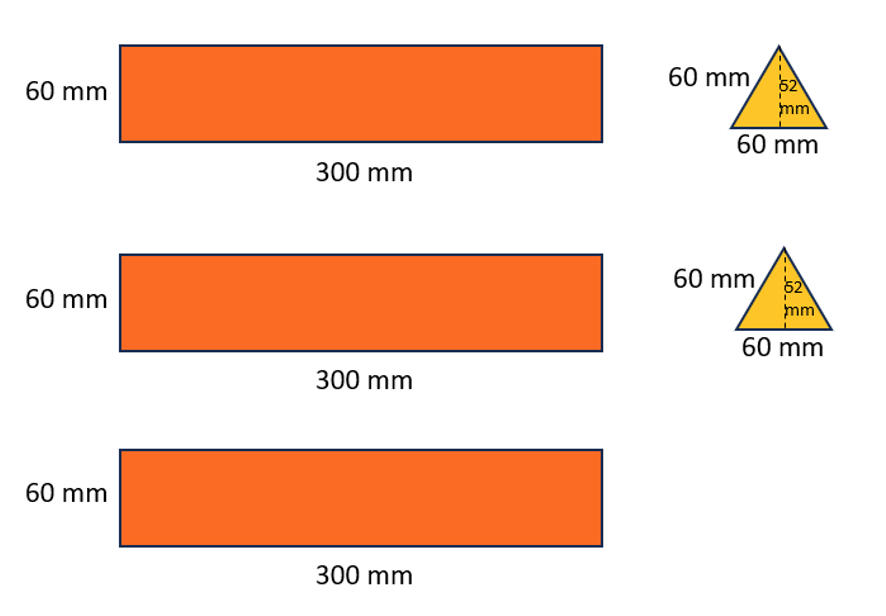
From here, a student might estimate by calculating only the areas of the rectangles because they appear to account for most of the surface area. (How many ways can you think of to find the total area of the three rectangles?) How close does considering only the rectangles get us to being able to choose an answer?
2. Rearrange the shapes. When we need to find the areas of unusual shapes, we can cut them up into more familiar ones. We can also put shapes together into more familiar shapes. A student might reduce the number of calculations they need to do by combining the rectangles into one large rectangle and combining the triangles into a new shape.
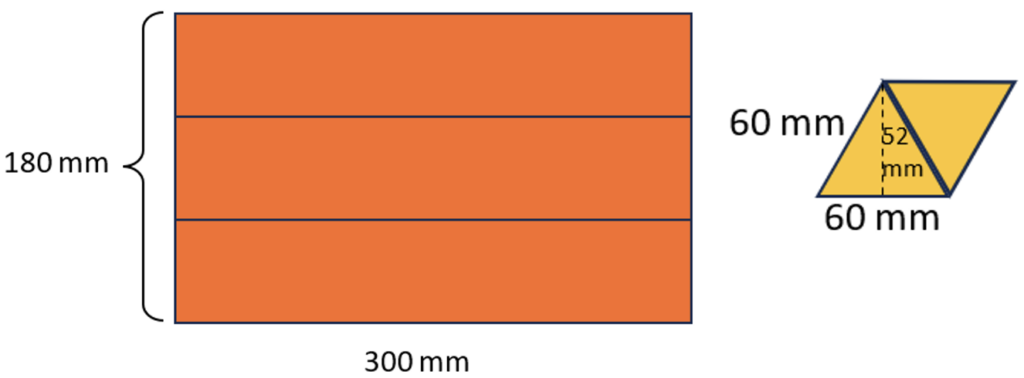
Where does the 180mm come from? How might this simplify finding the total surface area? What shape is formed by the two triangles? (Even if this strategy is not the first thing students think of when finding surface area, exploring it can help forge connections between area formulas and deepen conceptual understanding about area, specifically that area is additive (standard 3.MD.7d in the College and Career Readiness Standards), meaning that the area of a shape made of smaller shapes is equal to the sum of the areas of the smaller shapes.)
3. Think about what’s visible and invisible. Another option is to find the areas of only the visible parts of the box and then think about how much of the whole box they represent. On tests, and in life, we often don’t need to do all the work or find exact answers. In this case, we can clearly see one rectangular surface and one triangular surface. A student struggling to make sense of a two-dimensional picture of a three-dimensional object might just find the areas of those surfaces that are clearly labeled and visible. The area of the one rectangular surface that’s showing is 18,000 square millimeters and the area of the triangular surface that’s showing is 1,560 square millimeters. That’s 19,560 square millimeters of surface area already. Do you think that the visible parts are more than half, less than half, or about half of the total surface area? How would that help with choosing a reasonable answer choice?
Geometry tasks can be addressed starting with conceptual understanding instead of starting with formulas. The formula sheet can feel like a gift and a time-saver, but it can also feel like alphabet soup, with lots of letters that can make your head swim. And while it is a way in to tasks involving geometry concepts, it is not the only way. On the GED formula page, the formula that applies to this question is the one for a “right prism” and it reads: SA = ph + 2B. At the bottom of the section containing that formula is the note: p = perimeter of base with area B. (The HiSET formula page doesn’t have surface area formulas.) In the case of this question, applying the formula feels like a heavier lift, cognitively, than starting with the broader and more conceptual understanding of the meaning of surface area as how many square units (in this case square millimeters) it would take to cover the object. And ultimately the amount of calculation to be done is the same or less than what would need to be done if using the formula. If students develop conceptual understanding of area, perimeter, surface area, and volume before learning formulas, they will be equipped to use the formulas strategically or to find solutions in their own creative ways.

Sarah Lonberg-Lew has been teaching and tutoring math in one form or another since college. She has worked with students ranging in age from 7 to 70, but currently focuses on adult basic education and high school equivalency. Sarah’s work with the SABES Mathematics and Adult Numeracy Curriculum & Instruction PD Team at TERC includes developing and facilitating trainings and assisting programs with curriculum development. She is the treasurer for the Adult Numeracy Network.
