Ranked-choice voting: How does it work?
by Donna Curry
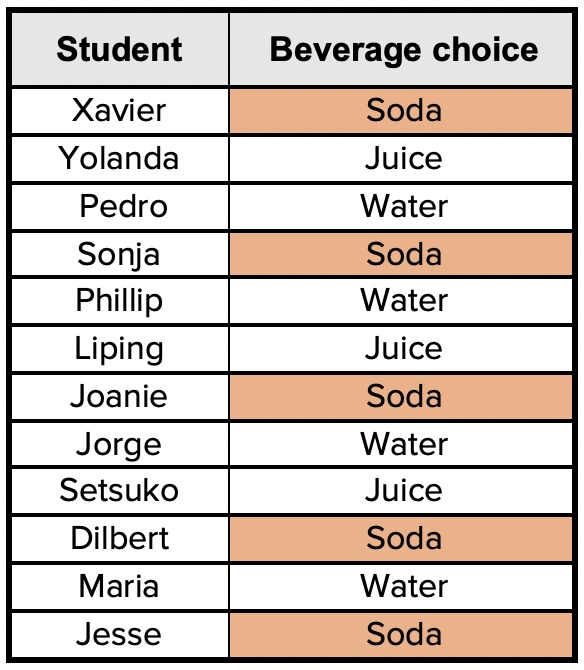
Imagine that it’s the end of the school year and you’re planning a class celebration with food and drinks. You ask your students to choose which beverage they’d prefer: juice, water, or soda. The students respond as follows:
So, you decide to go with soda for everyone since more students preferred that to juice or water.
During the party, you realize that less than half of the students drank any soda! They either drank from the water fountain or didn’t drink anything. What you didn’t realize is that maybe those few who wanted juice may have preferred water to soda. But how could you have known that? That’s where ranked-choice voting could have come in handy.
There’s a myth that ranked-choice voting means some people’s votes don’t count, but that’s not accurate. In this system, even if a voter’s top choice doesn’t win out, his or her next-favorite choice might. Had this voting method been used in the class party example, all of your students would have had a chance to vote for their favorite beverage as well as their second- and third-favorite (if they had wanted to).
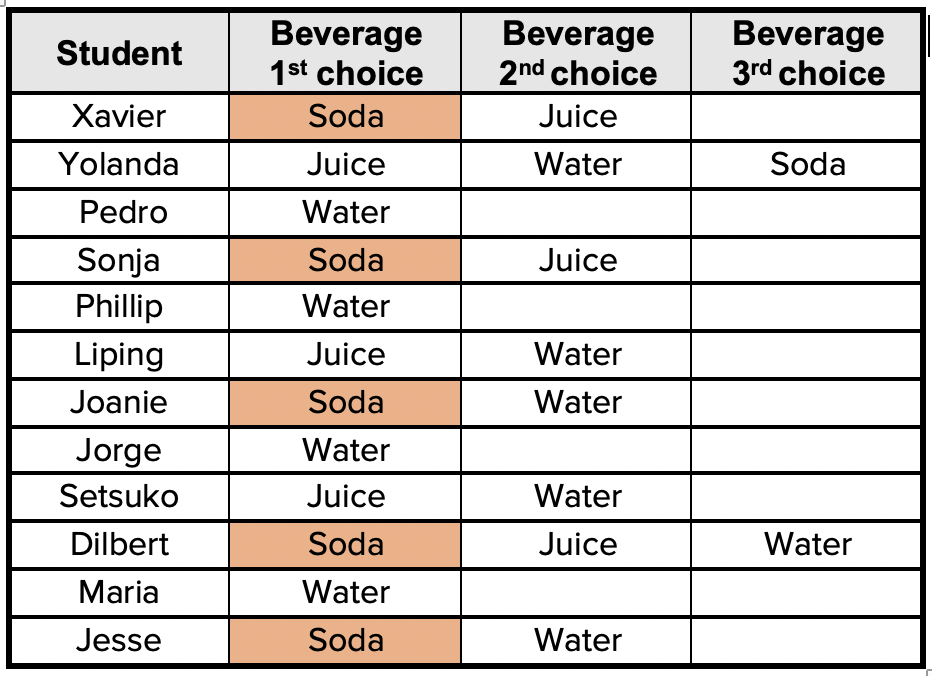
Had ranked-choice voting been used, the results might have looked like this:
As you can see, 5 of the 12 students chose soda as their first choice. But, the majority of students didn’t want soda – 7 of the 12 chose something else instead (water or juice). In ranked choice voting, you have to have a majority to ‘win’, even if it’s only to choose a beverage. You can also see that not everyone voted for a 2nd or 3rd choice. That is absolutely fine! What you cannot do is vote for a choice more than once. So, even if a student absolutely loved soda and nothing else, she could only vote once for soda.
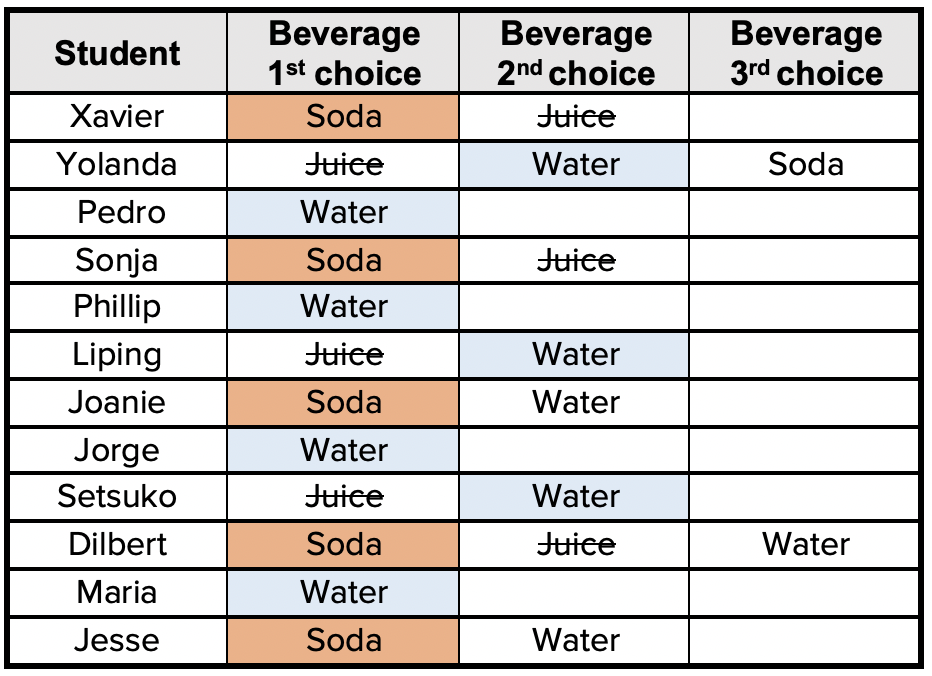
In ranked-choice voting, if no first-choice option wins a majority of votes, the option that received the fewest votes is removed from consideration. In this case, juice was the ‘loser’ because it received only three votes. But, the people who voted for juice still get to have a say in the result if they indicated a second-choice option. Now we can compare the 2nd choice votes with the 1st choice votes.
If you tally the first choices along with the second choices of the ‘loser’, you see that there are now seven votes for water. Since seven is more than half, the majority – people who are OK with drinking water – wins. If you had used this process, you would have discovered that most of your students would have preferred to have water instead of soda and your party would have been more of a hit.
So, to reiterate a few key points about ranked choice voting:
- The winner has to be an acceptable option to a majority of those voting. It’s not enough for the ‘winner’ to just have more votes than the second-place option – the winner has to get more than half of the total vote. That means, the winner has to receive at least 50% + 1 vote.
- Everyone’s vote counts. Sometimes a person gets to have a result he or she can accept even if it’s not his or her top choice.
- People do NOT have to vote for more than one option, but they also cannot vote multiple times for their favorite option.
The beverage example shows that sometimes the option with the most votes is not always what the majority of people really want. There are several times in recent U.S. history when a presidential candidate did not get the majority of votes. For example, in 2016, neither Hillary Clinton nor Donald Trump received the majority of votes in twelve states because a third-party candidate received some of the votes that would have gone to one or the other.
Probably the most significant example of how ranked-choice voting could have had an impact on the presidential election is in 2000 when almost three million voters in Florida chose Ralph Nader over Al Gore and George W. Bush. Had those three million voters had a second option, we may have had a different president. Whenever we have more than two political candidates in the same race, often people have to make the hard choice between the candidate that they personally prefer versus the candidate who has the best chance of getting the most votes. In a ranked choice voting system, people wouldn’t have to make that hard decision.
Most recently, the January 2021 run-off election for two Georgia senate seats could have been a lot simpler – and quicker – had ranked choice voting been used. (As a reminder, because neither candidate received a majority in the November 2020 election, per state law there had to be a run-off.) If those voters whose top choice came in third in the November election had had a chance to indicate their second choice, those votes could have been tallied to help give one of the two leading candidates enough votes to win, eliminating the need for a separate run-off election.
As with any election system, ranked-choice voting has pros and cons. [Consider all of the issues regarding the electoral college system, especially in the 2020 election year!] To read more on the pros and cons, read the New York Times article New York City Voters Just Adopted Ranked-Choice Voting in Elections. Here’s How It Works.
To help your students gain a better idea of how ranked-choice voting works, you might have them participate in an activity similar to the one illustrated in this short, easy-to-understand video How does ranked-choice voting work?
Donna Curry is an educator, curriculum developer and professional development specialist with over 30 years of experience in adult education. For the past 30+ years, she has focused on math standards development at the national level (Equipped for the Future National Standards and Standards-in-Action projects) and at the state level (including states such as Rhode Island, Washington, Oregon, New Jersey, Oklahoma, and Ohio). She has also worked on the National Science Foundation’s EMPower project and served as co-director for the NSF-funded Teachers Investigating Adult Numeracy (TIAN) project. She co-developed and implemented the Adult Numeracy Initiative (ANI) project and Adults Reaching Algebra Readiness (AR)2. Donna currently directs the SABES Mathematics and Adult Numeracy Curriculum & Instruction PD Center for Massachusetts and the Adult Numeracy Center at TERC.