Blog

Will This Be on the Test? (February 2025)

by Aren Lew

---

Welcome to the latest installment of our monthly series, “Will This Be on the Test?” Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually.

---

Welcome back to our continuing exploration of how to bring real conceptual reasoning to questions students might encounter on a standardized test.

It’s chilly here in Massachusetts as I’m writing this, so my thoughts are with the thermometer. Here’s a question for this month.

Here are some possible approaches:

1. Use an approximate story table. Equations and formulas tell stories. Keeping track of the plot in a story table can make navigating a complicated expression more accessible. In this case, the formula may seem especially intimidating because of the fraction 5/9, which is not the friendliest. However, a student who is comfortable with benchmark 1/2 may recognize 5/9 as being close to 1/2 and consider simplifying the story as a way of getting a good estimate. They might tell the story this way:

• First, subtract 32.
• Then, take about half of that.

What understandings are necessary to interpret the formula this way?

In a story table, that could look like this:

F	F – 32	Half of (F – 32)
50	28	14
20

(I’ve filled in an example calculation using 50 degrees Fahrenheit and left the row for 20 for you, but in a test situation a student could just go right to the calculation they need. Note that as you work a story table from left to right, each column applies a single calculation to the result of the previous column.)

2. Use a more precise story table. Another option is to navigate the story precisely as it is told, with the less friendly fraction. Which of these story tables do you think would work for finding a more precise answer? (Try filling them in to see if you’re right! Were there any surprises for you? How can you make sense of what did or didn’t work?)

F	F – 32	(F – 32) x (5/9)
20

F	F – 32	(F – 32) x 5	[(F – 32) x 5] ÷ 9
20

F	F – 32	(F – 32) ÷ 5	[(F – 32) x 5] x 9
20

F	F – 32	(F – 32) ÷ 9	[(F – 32) ÷ 9] × 5
20

F	F – 32	(F – 32) × 9	[(F-32) × 5] ÷ 5
20

You can learn more about story tables here: https://nyccami.org/story-tables/

3. Estimate by sketching out the action on a number line. Another way to make sense of the formula as a story is to sketch the story on a number line like this:

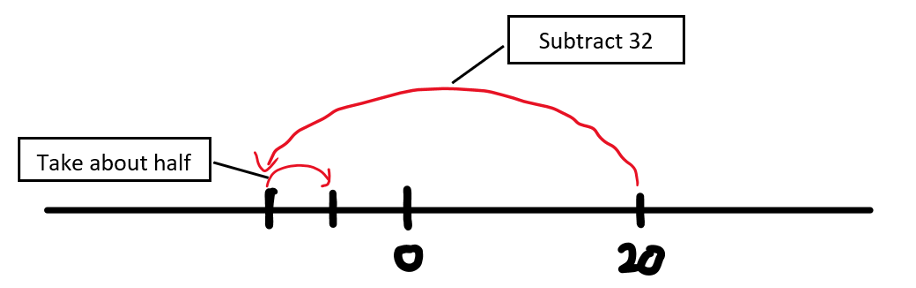
Even without figuring out the values at the unlabeled tick marks, you might be able to see which answer choice or choices are reasonable.

There is another way of approaching this question that involves simply relying on a sense of how the temperature scales relate, a sense you may be more likely to have if you have lived both inside and outside the United States. Beyond a having a ready frame of reference if this happens to come up on the test, having an understanding of the relationship between the two temperature scales that goes beyond memorizing the conversion formulas is both valuable and accessible. It is valuable to those of us who are more familiar with Fahrenheit to understand Celsius because climate science is often discussed in the Celsius scale. It is valuable to all of us because it helps us communicate better and understand each other. Here are a few ideas that might help you feel more comfortable with whichever scale is not the one you grew up with.

• 1 degree Celsius is about twice as big as 1 degree Fahrenheit. Conversely, 1 degree Fahrenheit is about half as big as 1 degree Celsius. This means that a change of, for example, 10 degrees represents a bigger change if you are in the Celsius scale and a smaller change if you are in the Fahrenheit scale.

• The equivalent temperatures 0 degrees Celsius and 32 degrees Fahrenheit are cold! (In fact that’s the freezing point of water.)

• The equivalent temperatures 32 degrees Celsius and 90 degrees Fahrenheit are hot! (At least to this New Englander.)

• -40 degrees Celsius is the same temperature as -40 degrees Fahrenheit. And that is extremely cold!

Here’s a bonus for you this month: This Desmos Classroom Activity created by the SABES team will provide an opportunity for you and your students to reason about the temperatures scales and develop more familiarity with them.

---