Blog

An Interview with Dr. Brooke Istas

by Connie Rivera

Dr. Brooke Istas is an instructor of Mathematics for Cowley College since Fall 2014. Prior to accepting the position, she acted as the Instructional Coordinator and a Mathematics Instructor for the Cowley College Adult Education and College Preparation Program. She is also the online moderator for the U.S. Department of Education, Office of Career, Technical and Adult Education (OCTAE), Literacy Information and Communication System’s (LINCS) Community of Practice for both Math and Numeracy and Correctional and Reentry Education communities. Also for the LINCS National Professional Development Center, she is certified as a National Trainer in math and numeracy and serves as a Subject Matter Expert Reviewer vetting math and science resources for the LINCS online Resource Collection. Read Brooke’s full bio here or visit her LinkedIn profile page.

Can you share how you became familiar with strategies for ELLs in Math Class?

The town I taught in has a large support network for immigrants, so the ESOL classes are large. Many intermediate and advanced ESOL students dual enroll in an Adult Basic Education class and an ESOL class. As a former special education major, I have always studied ways all my students can reach the same high-level goals (Universal Design for Learning – UDL).

What are some of the most effective strategies you use to teach numeracy to adult English learners?

I have so many answers to this question! Instructional routines allow students to focus on the content because how the activity works stays the same. Which One Doesn’t Belong? is one of my favorites because I can elicit the words students will need for the upcoming lesson from them before we begin.

Mathematical Language Routines give a framework for collecting students’ language and displaying it as a reference, giving students a hook and asking them for their questions, comparing and contrasting, and so much more.

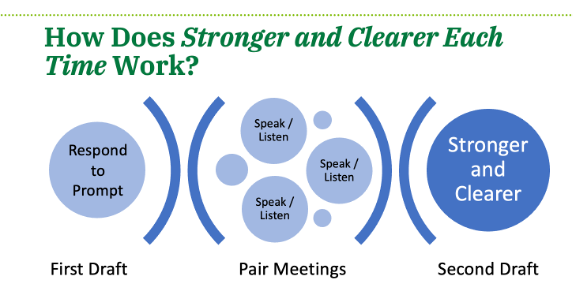
Figure 1: Stronger and Clearer Each Time

Giving students physical and virtual objects to move (manipulatives, but also words or images that need sorting, categorizing, or hanging on a number line) lowers the need for specific English words to participate.

Inevitably I’ll say an unplanned something that needs an image, so I have Google Images handy to display a collage of images that illustrate a word.

I encourage first or common languages to be spoken in class. When our goal is to understand a concept, it can be explored in any language. (A core principle of UDL: be tight to the goal, but flexible on the means.) Once the ideas are developed, they can be put into English.

How do you integrate numeracy instruction with language learning?

Integrating numeracy instruction with language instruction is easier if you start with a context and take the math from there.

Student-centered learning means numeracy and language happen together naturally. Learner-centered instruction includes choosing non-routine, open problems that present opportunities to explore and discover something. Students may be asking questions, doing research, and discussing strategies and ideas (rather than sharing answers). They make decisions and justify them with math. They estimate, predict, and analyze.

What are some common challenges adult English learners face in acquiring numeracy skills?

Like many students, there is often a disconnect in realizing how their life knowledge applies to school math. Fractions are sometimes puzzling since there is much more of a focus on them in school and society in the US than there is in other countries.

As teachers, we sometimes assume some contexts are common to everyone that are not. One example of this is time—I have had students whose days were marked by before and between prayer bells that rang in the village, not time on a clock. Over time, I learned to make fewer assumptions.

How do you help students overcome math anxiety or negative attitudes towards learning numeracy?

I’m open about my numeracy struggles and journey with my students. It helps students to hear that math isn’t magic and tricks and that you can struggle and still learn.

I select problems with multiple correct answers (often involving decision-making like Would You Rather?). I’m genuinely interested in their thinking, and our focus is on strategies and curiosity rather than answers. I never expected timed solutions.

Can you share a success story of a student who significantly improved their numeracy skills through your teaching methods?

Fatima* always comes to mind when I think of students who thrived in my Adult Basic Education class. Fatima was a mom of 5 (now 6), a refugee from a country where minimal formal schooling is given to girls. Her appraisal scores in both reading and math showed results with only a few correct answers. Her speaking and listening skills are far higher than her reading, and she is an expert learner who is very comfortable sharing rough draft thinking and thinking deeply. The whole class thrived with her there.

The students and I had decided on the unit, How Grand Is Your Total? to address many of their requests for learning this semester. Several students could not attend the first 15 to 30 minutes of class each day because of their children’s schedules, and absences were fairly common. Each night before class, I posted our initial problem to Google Classroom so all students would have access to the materials no matter when they could attend classes. Several of the students, including Fatima, used that as an opportunity to try the problem before class so they would have enough think time.

We completed division, and I hadn’t introduced fractions yet. I remembered that several students had requested fractions as a topic for the semester, and most were unfamiliar with them. As usual, I posted the problem for the next day, but this time, expecting silence until class since I thought it was a new topic:

In the morning, I had a text from Fatima:

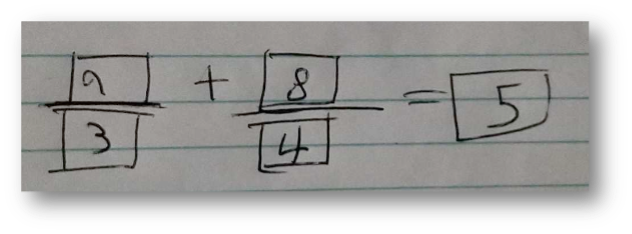
I wrote back to her saying, “Yes!, this is an answer to the problem,” and expressing confusion because I thought she told me she didn’t know about fractions—and here she was adding fractions before the lesson. She wrote back to me, just as confused and wondering why I didn’t remember that I had taught them already. I had to wait for class for an in-person conversation so she could make me understand that I had taught her everything she needed to know in our division lessons.

Wow. My formal education was getting in the way of my thinking. The standards say, “Build fractions from unit fractions by applying and extending previous understanding of operations on whole numbers.” and I knew that enough to set up the lessons in the way that I did, but I didn’t truly absorb it until Fatima taught me to see all the connections.

*name changed.                  

---